If you are citizen of an European Union member nation, you may not use this service unless you are at least 16 years old.
You already know Dokkio is an AI-powered assistant to organize & manage your digital files & messages. Very soon, Dokkio will support Outlook as well as One Drive. Check it out today!

A1-D-1-3

Page history last edited by Tashe Harris 6 years, 2 months ago

A1.D.1.3 Interpret graphs as being discrete or continuous.

In a Nutshell

Students will learn that a discrete graph is one in which the data can only take on certain values, for example, integers and a continuous graph is one in which data can take on any value within a specified interval (which may be infinite).

Student Actions	Teacher Actions
Students will Develop Mathematical Reasoning to determine whether the ordered pairs of the graph should be connected, making it continuous. Students will Develop a Deep and Flexible Conceptual Understanding of discrete being only a finite set of points and continuous is an infinite set of points. Students will interpret a real world application into a graph and Make Conjectures, Model, and Generalize whether is it discrete or continuous and vice versa. Students will Communicate Mathematically while justifying their reasoning for a graph being discrete or continuous.	Pose purposeful questions for students to distinguish between discrete and continuous graphs and real world applications. Facilitate meaningful mathematical discourse to encourage and expert students to make connections between the real world application and the graph. Elicit and use evidence of student thinking to direct students to justify their interpretations of solutions. Encourage productive struggle as students explore and discuss the data to distinguish the difference between discrete and continuous graphs.
Key Understandings	Misconceptions
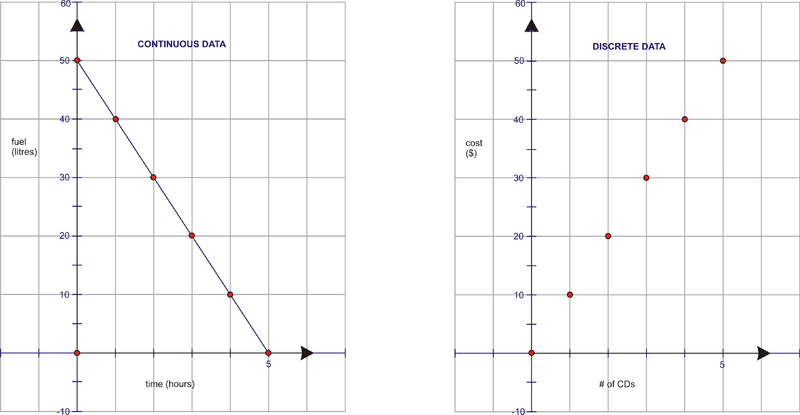
The graph of a discrete function, only separate, distinct points are plotted, and only these points have meaning to the original problem. A discrete graph is a series of unconnected points (a scatter plot). The graph of a continuous function is drawn without lifting the pencil from the paper. A continuous graph allows the x-values to be ANY points in the interval, including fractions, decimals, and irrational values.	Students may confuse the words discrete and continuous as these are new vocabulary words for this grade level. When a graph is continuous on just an interval (section of the Real Numbers), students may consider it to be discrete instead of continuous on the interval. When given a real world example, students may have difficulty determining whether the graph is discrete or continuous. Students do not recognize that in a discrete graph, each x,y pair is a distinct point while in a continuous graph,the points are connected.